简介

  • 很常见的流密码

    • 现实世界被认为是弱加密方式

  • 但事实上，并没发现任何明确的漏洞

    1. Bit-flip-attack这种，原理上没什么用的攻击
    2. 针对与RC4结合使用的协议特征的攻击

  • 需要很多密文进行分析

    • 如果密文量不足，RC4仍然不切实际(短时间内)不可解读
    • 常规CTF问题，量及时间都很困难

  • 因此，RC4题目还能在CTF中存活

RC4算法

由两个元素组成

  1. KSA(Key-scheduling algorithm 密钥调度算法)
    • 从key创建表的过程
  2. PRGA(Pseudo-random generation algorithm 伪随机生成算法)
    • 在更新表时生成伪随机数序列的过程
  • 实际使用时，经常结合IV(Initialization Vector 初始化向量)使用
  • 这用于防止相同的明文在使用相同的密钥加密时产生相同的密文(类似linux密码中的salt)
  • 类似的，在解密时，从密钥生成伪随机数序列并对密文进行xor异或

1.KSA(生成表)

最终生成的S是RC4的状态表，因为只对S进行交换处理，最终将重新排列[0,1,2,…255]

2.PRGA(生成伪随机数)

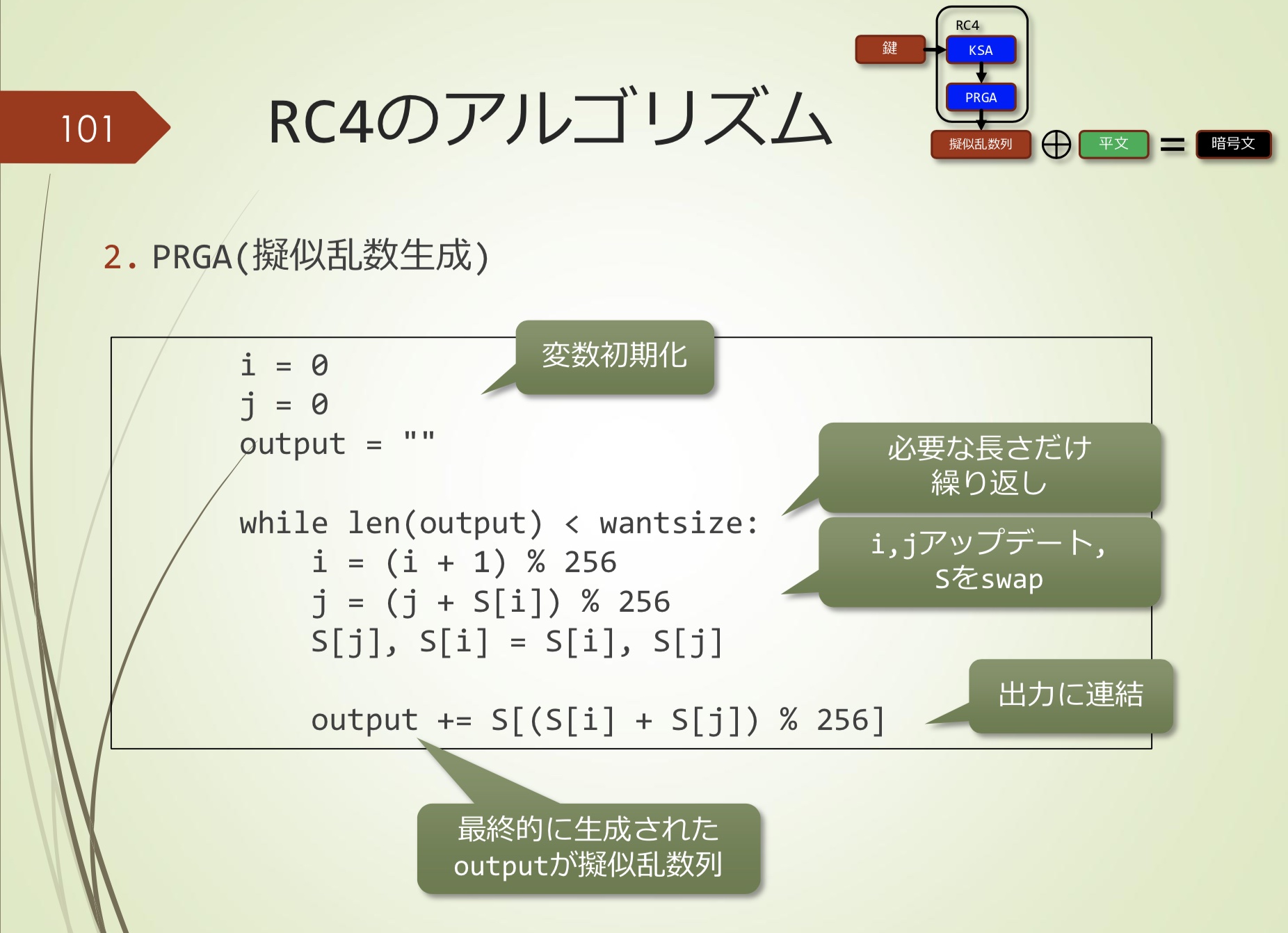
  • 最终的output是生成的随机数序列
  • 由于密钥未在PRGA中使用（密钥已经反映在S中），如果作为RC4内部表的S泄漏，则可以识别出随后的伪随机数序列

关于RC4实现

  • RC4通常由KSA和PRGA实现为单独的函数
  • 表S由KSA或PRGA使用
    • 也就是说，它通常被定义为全局变量（= .bss）
  • 通过argv[0] leak获取全局变量中的密码